黄小林,李粮杰,张燕宁,郝稀奇
(桂林电子科技大学 建筑与交通工程学院,广西 桂林 541004)
石墨烯以其高强、轻质的特性成为优异的增强材料[1]。将石墨烯纳米片沿基体材料某一个或多个方向连续梯度分布而制成的功能梯度石墨烯增强复合材料(functionally graded graphene platelets,FG-GPLs),在航空航天、机械、交通、土木工程等领域有广阔的应用前景。因此,近年来,对FG-GPLs结构力学特性的研究受到了极大关注[2-5]。
文献[6]用有限单元法研究了热环境下FG-GPLs层合板/壳的振动响应,发现热荷载会引起结构应变畸变,进而影响其固有频率。文献[7]通过微分求积法,分析了不同边界条件下FG-GPLs圆柱壳和环形板的自由振动和静力弯曲,提出了当石墨烯纳米片的长宽比和长厚比处于一定范围时,可忽略其形状对结构刚度的影响。文献[8]基于一阶剪切变形理论,建立了FG-GPLs截锥中厚壳的振动方程,研究了石墨烯分布模式和质量分数对结构非线性振动的影响。
由于制造工艺的缺陷,在制备FG-GPLs结构过程中不可避免会产生孔隙,因此,研究含孔隙结构的FG-GPLs的动力学特性很有必要。文献[9]考虑了含内部孔隙的FG-GPLs梁的振动响应和弹性屈曲行为,提出了高斯随机场下多孔结构的力学模型,建立了泊松比和孔隙的对应关系。根据开孔泡沫金属模型,文献[10]用伽辽金(Galerkin)法和四阶龙格库塔法研究了弹性地基上多孔FG-GPLs板的非线性振动和动态屈曲问题,并通过试验确定了孔隙对板结构的影响规律。文献[11]基于克希霍夫-拉夫(Kirchhoff-Love)壳体理论,用瑞丽里兹(Rayleigh-Ritz)法研究了FG-GPLs圆柱壳的自由振动,发现边界条件和孔隙同时对壳体的力学响应有显著影响。文献[12]以虚拟弹簧刚度模拟同边界条件,基于一阶剪切变形理论计算了外部激励下FG-GPLs圆柱壳的受迫振动,提出了刚度阻尼因数比质量阻尼因数对动挠度幅值的影响更大。文献[13-14]分别用傅里叶微分求积和广义微分求积法计算了多孔FG-GPLs截锥壳的固有频率,发现壳体厚度与固有频率近似线性相关,而且孔隙对固有频率的影响不可忽略。
可见,目前关于FG-GPLs构件力学行为的研究中,对板/梁结构研究的较多[15-17],而对圆锥壳特别是含孔隙的圆锥壳的研究则较少。这是因为,一方面,圆锥壳的静/动力平衡方程为变系数的高阶偏微分方程,求解困难;另一方面,含孔隙的石墨烯增强功能梯度材料物性参数的计算方法比较复杂,不易理解。因此,本文先假定孔隙的体积组分,基于传统多孔材料物性参数的模型计算FG-GPLs材料的物性参数。然后,考虑周围弹性介质的影响,建立弹性介质中FG-GPLs截锥壳振动的控制方程并求解。最后,详细讨论孔隙、石墨烯、弹性介质等因素对振动频率和动力响应的影响,为此类结构的优化提供理论基础。
弹性介质中的截锥壳如图1所示,弹性介质中含内部孔隙的石墨烯增强材料(FG-GPLs)截锥壳受横向动荷载q(s,θ,t)作用。壳体厚度和母线长度分别为h和L,截锥壳的小头半径、大头半径和半锥角分别为R1、R2和γ,s、θ和z方向的中面位移分别为u、v和w,顶点到截锥壳上端和下端的距离分别为S1和S2,弹性介质的压缩刚度和剪切刚度分别为Kw和Kp。假设截锥壳由基体材料和增强相石墨烯纳米片组成。石墨烯纳米片和内部孔隙在壳厚度方向均连续分布。图2为孔隙的分布类型。孔隙分布归纳为4种类型:(a)T1为离中面越远孔隙越少的对称分布;
(b)T2为离中面越远孔隙越多的对称分布;
(c)T3均匀分布;
(d)T4为从内侧到外侧孔隙越来越少的分布。
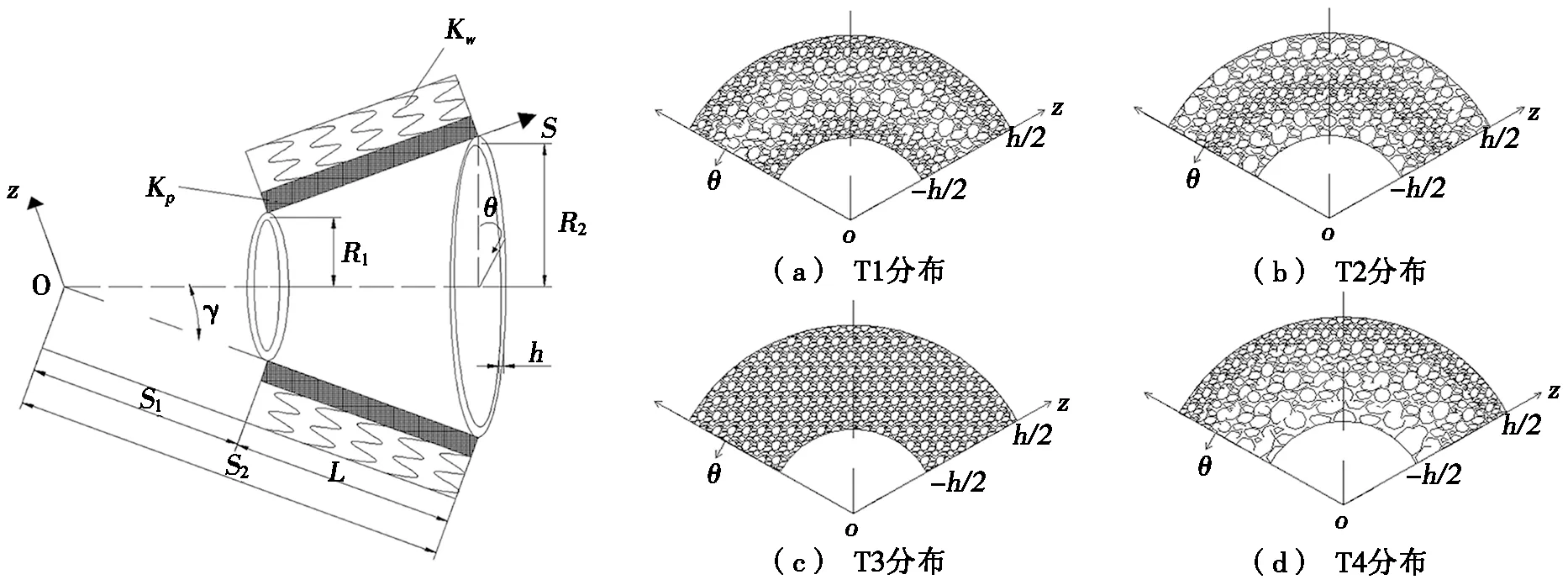
图1 弹性介质中的截锥壳 图2 孔隙的分布类型
设孔隙的体积组分沿厚度的分布为[10]:
(1)
其中:e0,e1,α和e2分别为T1,T2,T3和T4分布的孔隙系数。
此截锥壳的弹性模量、剪切模量和泊松比用混合律可表示为:
E(z)=E0(1-VP);
(2)
G(z)=G0(1-VP);
(3)
v(z)=v0(1-VP),
(4)
其中:E0,G0和v0分别为无孔隙时截锥壳的杨氏弹性模量(Pa)、剪切模量(Pa)和泊松比。
假设质量密度为:
(5)
其中:ρ0为不含内部孔隙的石墨烯增强截顶圆锥壳的的密度;
em0,em1,α′和em2为质量密度系数。
(6)
从式(6)可看出:给定孔隙体积的分布系数e0,e1,α和e2,可分别计算质量密度的孔隙系数度em0,em1,α′和em2。
假设各种孔隙分布板的质量相同,有:
(7)
根据修正的Halpin-Tsai细观模型,无孔隙的FG-GPLs截锥壳的有效弹性模量可表示为:
(8)
其中:Em为基体材料的弹性模量;
VGPL为石墨烯的体积组分;
ξL,ξW,ηL和ηW定义为:
(9)
无孔隙的FG-GPLs截锥壳的泊松比和密度用混合律可表示为:
ν0=νGPLVGPL+νm(1-VGPL),ρ0=ρGPLVGPL+ρm(1-VGPL),
(10)
其中:ρGPL和νGPL分别为石墨烯的质量密度和泊松比;
ρm和νm分别为基体材料的质量密度和泊松比。
无孔隙的FG-GPLs截锥壳的剪切模量为:
(11)
假设石墨烯沿壳厚度有3种分布类型(见图3)。其中,(a)G1为石墨烯数量由内、外侧向中面逐渐减少的分布。反过来,(b)G2为内、外侧向中面逐渐增大的分布。而(c)G3为均匀分布。3种分布石墨烯的体积组分VGPL假设为:
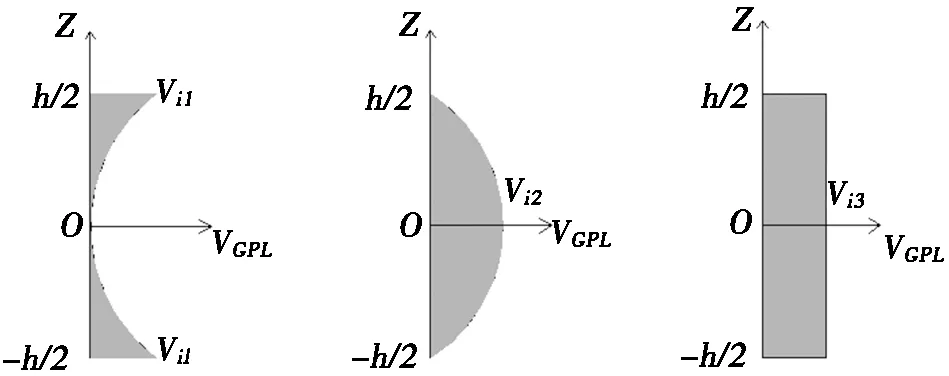
(a) G1分布 (b) G2分布 (c) G3分布
(12)
其中:Vi1,Vi2和Vi3分别为G1,G2和G3石墨烯分布下体积分数的最大值。
设3种分布类型的石墨烯总体积分数相等,则有如下关系式:
(13)
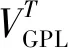
(14)
假设截锥壳在变形过程中始终与弹性介质紧密接触,且忽略其阻尼与惯性力的作用,则弹性介质对截锥壳的反作用力为[18]:
(15)
引入变量φ=θsin(γ)和应力函数F。应力函数与面内力的关系为:
(16)
令s=S1ex,F=F1e2x,基于Donnell经典薄壳理论和Hamilton原理,可推导此截锥壳振动的控制方程为:
(17)
L21(F1)+L22(w)=0,
(18)

设截锥壳的边界条件为两端简支,其动挠度的形式解为:
(19)
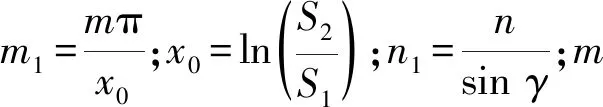
(20)
其中:系数Ki见文献[18],再将式(19)和式(20)代入式(17),两边同乘以exsin(m1x)sin(n1φ),得:
(21)
其中:W={W11,W12,...Wm1,n1...}T为动挠度列向量,M和K分别为质量矩阵和刚度矩阵;
q={q11,q12,...qm1,n1...}T为荷载列向量,且:
(22)

det(ω2M+K)=0。
(23)
当q(x,φ,t)≠0时,用Newmark数值积分法可求得其动挠度。本文采用的Newmark积分法的2个计算参数分为β=0.5,γ=0.25,时间步长Δt=0.001s。
表1计算了弹性介质中纯金属功能梯度材料(functionally graded materials,FGM)截锥壳的量纲归一化频率。基体材料镍和增强材料陶瓷的物性参数见表2。增强材料的体积分数在厚度的分布为:

表1 弹性介质中纯金属功能梯度材料截锥壳的量纲归一化频率

表2 材料物性参数
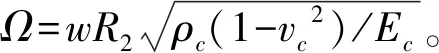
表3计算了含孔隙的石墨烯增强复合材料(FG-GPLs)圆柱壳的固有频率。当半锥角γ→0时,S1→∞,S1sinγ=R,S2=S1+L,x0=L/S1时,截锥壳退化为圆柱壳。壳体基体材料为钢,石墨烯纳米片的几何尺寸为长aGPL=2.5×10-9m,宽bGPL=1.5×10-9m,厚hGPL=1.5×10-6m,圆柱壳柱壳尺寸R=1 m,L/R=20,h=0.002R,石墨烯质量分数WGPL=1.0%。
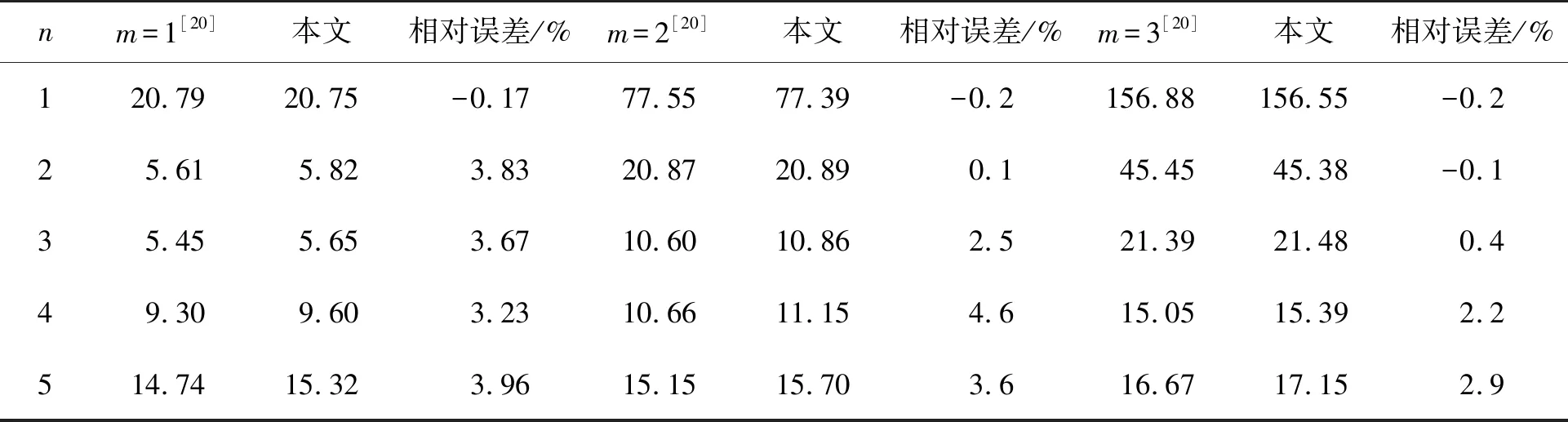
表3 含孔隙的FG-GPLs圆柱壳的固有频率 Hz
由表1和表3可看出:本文的计算结果和相关文献的结果是比较接近的。

表4和表5列出了不同孔隙分布和石墨烯分布、不同孔隙系数和弹性介质参数下截锥壳的量纲归一化频率。从表4和表5中可看出:4种孔隙类型的量纲归一化频率均随孔隙系数e0的增大而减小,而且T1分布的量纲归一化频率比其他3种分布都大,说明在4种孔隙分布中,T1分布对截锥壳整体刚度的削弱程度最小。在3种石墨烯分布中,G1分布的量纲归一化频率最大,G2分布最小,说明按G1分布植入石墨烯纳米片更能提高截锥壳的整体刚度。另外,量纲归一化频率随剪切参数Kp及压缩参数Kw弹性参数的增大而提高,而且两者比较,剪切参数Kp比压缩参数Kw提高的程度更为显著,说明在介质的弹性压缩和弹性剪切性质中,剪切变形的影响程度更大。例如,在孔隙分布和石墨烯分布为T1和G1,e0=0.1时,Kw从0增大到1.0,量纲归一化频率只提高5%。而Kp从0只增大到0.1时,量纲归一化频率却提高了7.6%。
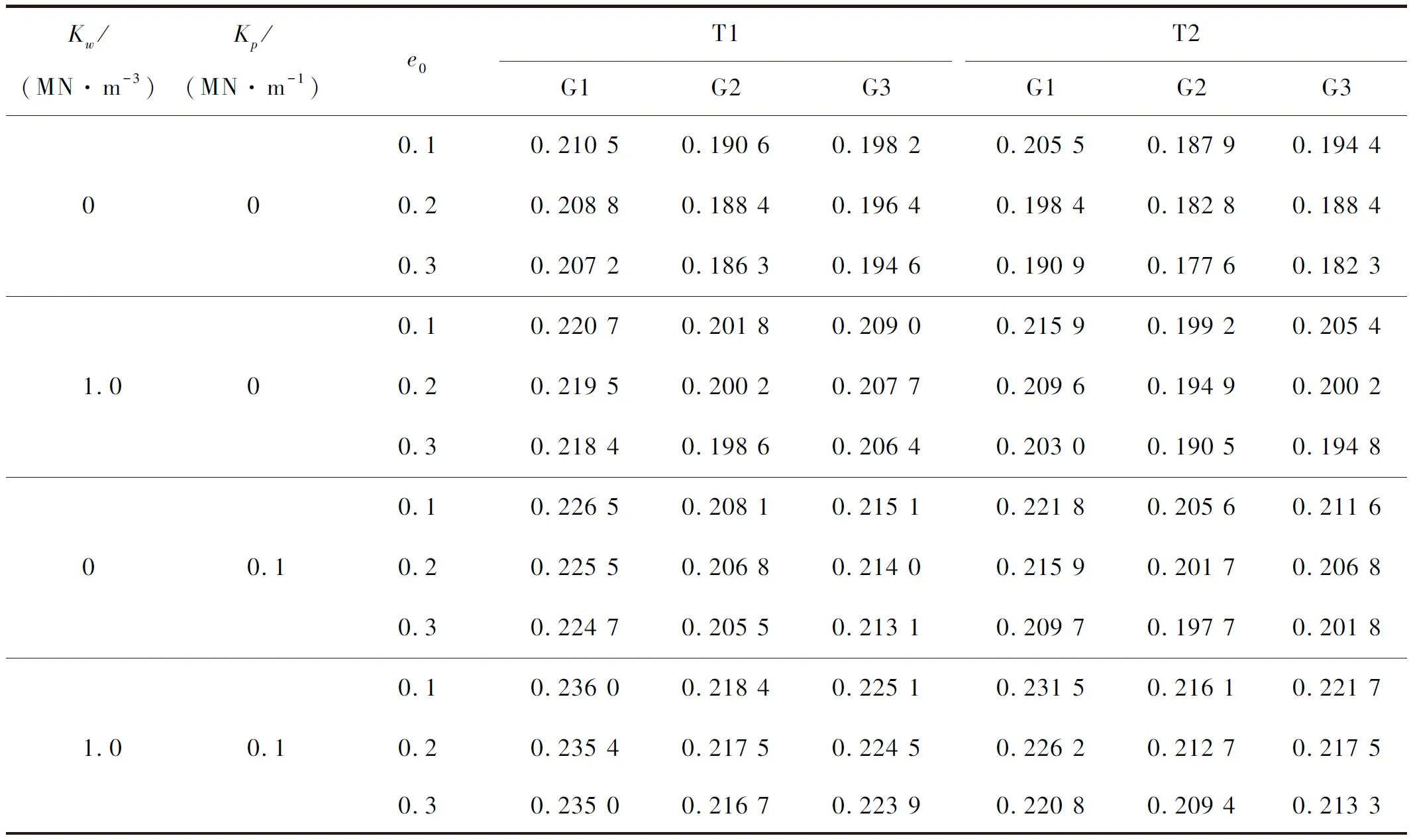
表4 T1和T2孔隙分布下FG-GPLs截锥壳的量纲归一化频率

表5 T3和T4孔隙分布下FG-GPLs截锥壳的量纲归一化频率
图4为T1和T3孔隙分布的量纲归一化频率Ω随石墨烯质量分数的变化曲线。由图11可看出:Ω随着石墨烯质量分数WGPL的提高而增大,而且WGPL越大,Ω的增长越快。以T1/G1为例,当WGPL=1.0%时,Ω约提高20.51%,说明添加少量石墨烯纳米片能显著提高截锥壳的整体刚度,这是因为石墨烯的弹性模量远比基体材料大而质量密度又远比基体材料小。此外,综合表4和表5可得:不同石墨烯分布类型的增长速度不同,G1最大而G3最小,再次证实了G1分布能更有效提高材料的整体刚度。

(a) T1分布
图5~图7计算了不同弹性介质参数、孔隙系数、石墨烯质量分数下截锥壳的动挠度,其中,横向动荷载q(s,θ,t)=8 000 sin(500t)Pa,动挠度的坐标点为(S1+L/2,π/2)。
由图5可看出:动挠度随弹性介质参数的增大而减小,对T1/G1类型,弹性介质参数(Kw,Kp)=(1,0)比(Kw,Kp)=(0,0)的动挠度幅值约低30.55%,(Kw,Kp)=(0,0.1)比(Kw,Kp)=(0,0)动挠度幅值约低47.37%,可见,同对量纲归一化频率一样,剪切参数Kp比压缩参数Kw的影响更显著,印证了介质的剪切参数对圆锥壳有限刚度的影响比压缩系数大。

(a) T1/G1
图6为孔隙系数对截锥壳动挠度的影响。从图6a中可看到:孔隙系数e0从0.1增大到0.3时,最大动挠度提高约14.7%,这是由于孔隙系数越大,孔隙率越大,圆锥壳的有效刚度变小。而在同为G1石墨烯分布的情况下,当孔隙系数e0=0.3时,T1孔隙分布的最大动挠度比T3分布的最大动挠度只小了8.52%,说明孔隙分布对动挠度的影响并不显著。
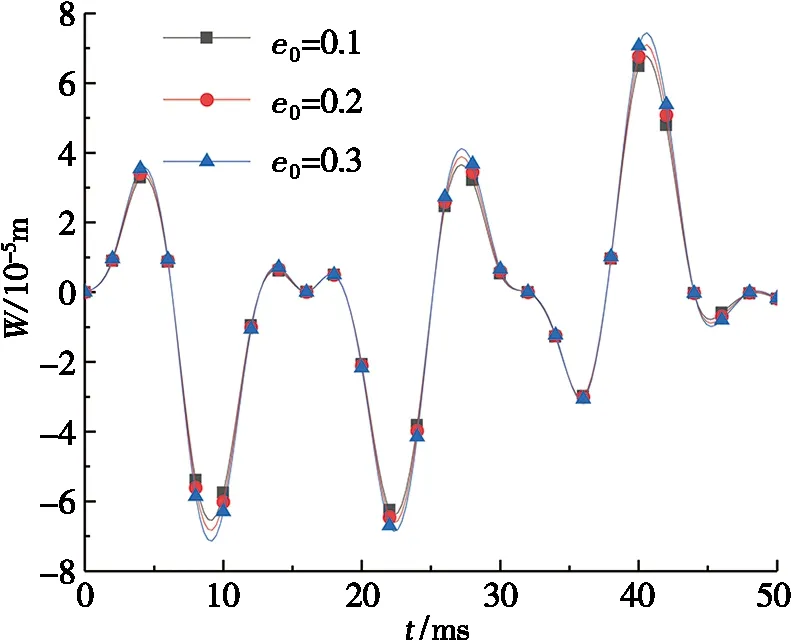
(a) T1/G1
图7为石墨烯质量分数对截锥壳动挠度的影响。从图7a和图7b可知:石墨烯质量分数WGPL从0%提高到0.6%,T1/G1类型的截锥壳的动挠度幅值减少约36.83%,T1/G3动挠度幅值减小约45.66%,石墨烯纳米片可显著提高截锥壳的整体刚度,因此,动挠度幅值随石墨烯质量分数的提高而明显减小。
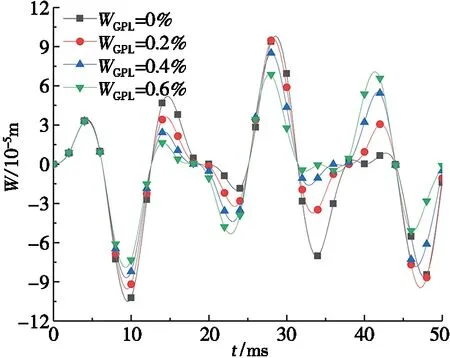
(a) T1/G1
(1)与孔隙系数相比,孔隙的分布类型对振动频率和动力响应的影响更为显著。由振动频率的结果可看出,在T1,T2,T3和T4 这4种孔隙分布类型的截锥壳中,T1的整体刚度最大,而T2的整体刚度最小。
(2)在基体材料中植入少量的纳米片可显著提高截锥壳的振动频率和降低动挠度的幅值,而且不同的石墨烯分布类型,其影响程度不同。在G1,G2和G3这3种石墨烯分布类型中,G1的影响程度最大,而G2最小,故T1孔隙分布和G1石墨烯分布截锥壳的刚度最大。
(3)弹性介质提高了截锥壳的振动频率,并且降低了动挠度的幅值。与压缩刚度参数相比,剪切刚度参数的影响更为明显。
猜你喜欢量纲挠度石墨量纲分析在热力学统计物理中的教学应用*物理通报(2022年6期)2022-05-27石墨系升温球的实践与应用昆钢科技(2022年1期)2022-04-19Spontaneous multivessel coronary artery spasm diagnosed with intravascular ultrasound imaging:A case reportWorld Journal of Clinical Cases(2020年16期)2020-09-16——以匀加速直线运动公式为例">浅谈量纲法推导物理公式的优势——以匀加速直线运动公式为例经济师(2020年8期)2020-08-18基于长期监测的大跨度悬索桥主梁活载挠度分析与预警科学技术与工程(2020年36期)2020-02-04科技论文编辑加工中的量纲问题学报编辑论丛(2018年0期)2018-02-21石墨烯在超级电容器中的应用概述通信电源技术(2016年6期)2016-04-20不同模量面板夹心泡沫铝板大挠度弯曲西安建筑科技大学学报(自然科学版)(2014年2期)2014-11-12基于形态学小波包降噪的管母挠度监测方法振动、测试与诊断(2014年4期)2014-03-01石墨矿中固定碳的分析与探讨中国非金属矿工业导刊(2014年3期)2014-02-28



